10 わり算と分数 整数の除法の商を分数で表す こと 分数と小数,整数の関係 11 小数のしくみとたし算,ひき算 1の位, の位の小数のよみ 方,表し方 小数の構成,相対的な大きさ *昔の小数の位のよび方 12 分数 分数の意味と表し方天秤の原理と反比例 principle of leverage;2分母と分子に同じ数をかけても値は変わらない 分母分子に2をかけても分数の値は変わらないように、繁分数の分母分子に 4 3 4 3 をかけても繁分数の値は変わりません。 以上を通して見ると以下のようになります。 2 3 ÷ 3 4 = 2 3 3 4 = 2 3 × 4 3 3 4 × 4 3 = 2 3 × 4 3 1 = 2 3 × 4 3 2 3 ÷ 3 4 = 2 3 3 4 = 2 3 × 4 3 3 4 × 4 3 = 2 3 × 4 3 1 = 2 3 × 4 3 また、繁分数にしなくても同じような

部分分数分解のやり方と公式 5パターンの問題から分かる変形のコツ アタリマエ
分数の仕組み
分数の仕組み-帯分数のたし算には、次のような計算の仕方があります。(ノートに書きましょう) ㋐ 帯分数を整数部分と分数部分に分けて計算する。 ㋑ 帯分数を仮分数になおして計算する。 ☆上のやり方を参考にしながら、練習問題をノートにしましょう。p86動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru



分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利
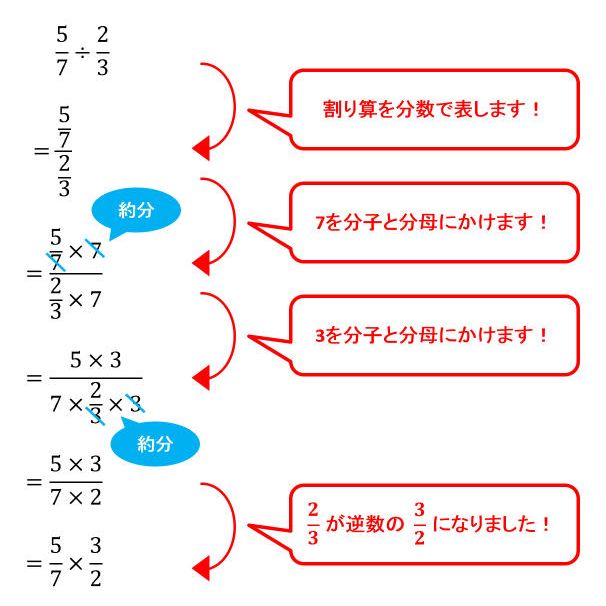
帯分数「2と3分の1」の数直線上の位置 数直線から分かる通り、仮分数 $\frac{7}{3}$ は、整数で2の位置から、さらに$\frac{1}{3}$ を足した数であることが分かります。よって、帯分数に直すと$2\frac{1}{2}$ となります。 まとめると、 1 × 01 = 1 ÷ 10 = 1 × となり、全て「 1 を 10個に分けたときの 1 個 ( 10個で 1 になる) 」という意味です。 同様に、 01 × 01 = 01 ÷ 10 = × なら、「 01 を 10個に分けたときの 1 個 ( 10個で 01 になる) 」なので「 001 , 」となります。 また、1 × 10 = 1 ÷ 01 = 1 ÷ という関係でもあります。 具体的な計算の仕方は「 整数に直して計算し、最後に小数点の計算分数のわり算を扱うときには「包含除」で考えることが理解するうえでの近道となります。分数のわり算は、以下のように計算しますね。 4 ÷ 2 5
分数 分数のしくみ 分数 分数のしくみ(2) 分数 いろいろな分数 分数 分数のたし算 分数 分数のひき算 分数 分数ゲーム 分数 分数ゲーム(対戦型) 分数 分数あつまれ!異分母分数 分数 分数あてクイズ 円と球 点があつまって円になるまた、分数の表し方について知ること イ 分数は、単位分数の幾つ分かで表せることを知ること。 ウ 簡単な場合について、分数の加法及び減法の意味について理解し、計算の仕方を 考えること。 を受けて設定された単元である。第2次 分数のしくみ 2時間 4 単位分数をもとにして、 分数の構成や大小比較につ いて理解する。 分数のしくみについて考 えよう。 分数の大きさに色を塗り比較をす ることで分数のしくみを考える。 1 6 lの6個分は何 でしょう か。
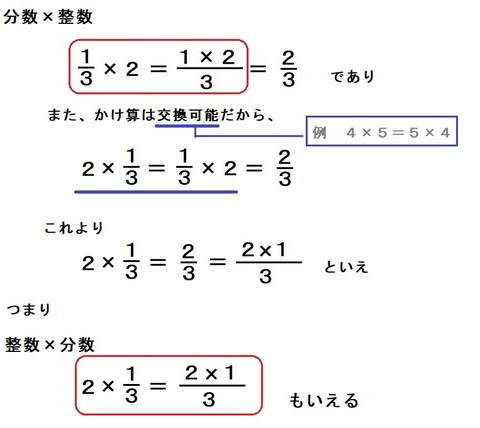
( )分( )秒 ミス( ) 仮分数を帯分数になおしましょう。 さくら社の公式サイトです。 横山験也著 326発売 想像の斜め上を行く手づくり教材が満載! 「不等号さかな君」「1L封筒」「お金つき数カード」「四捨五入ヘビ君」「小数点イカ」「カマキリライダー180°」etc長年の現場経験から培った、手軽に作れて驚くほど授業を効果的にする教材の分数 と整数 ,分数 と分数 のかけ 算とわり 算 (3)分数 ×整数 ,分数 ÷整数 ,分数 ×分数 ,分数 ÷分数 基本 の確かめ 分数 に整数 をかける 計算 では , 分母 はそのままで ,分子 に整数 を かければよい 。 分数 を整数 でわる 計算 では ,




ウチダ 教材総合カタログ 小学校



分数のわり算の仕組みを理解しよう 逆数をかけるのはどうして の謎に挑む 中学受験ナビ
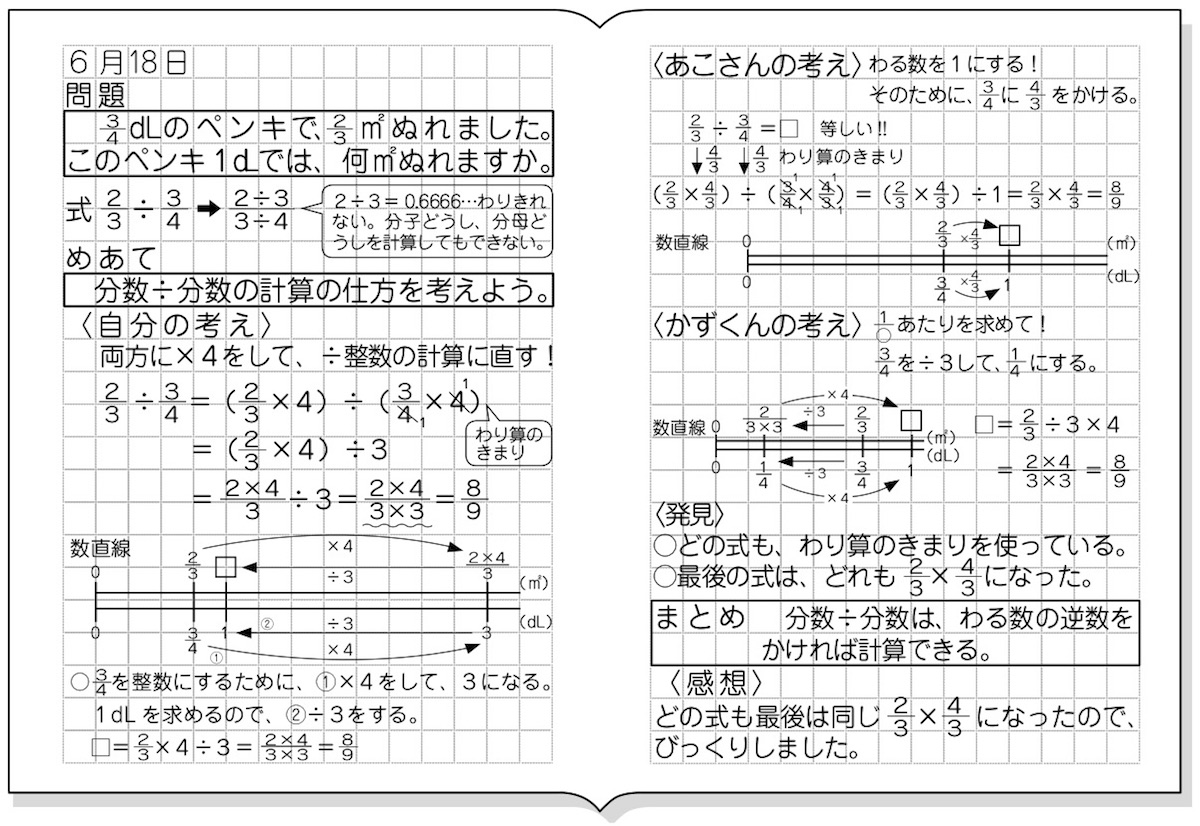
分数の掛け算はなぜ分母同士・分子同士をかけると計算できるのでしょうか? 小学6年生向けに分かりやすい方法を教えていきます。 目次 非表示 1 どんな計算も整数に直すことが基本 2 分数×整数分数÷整数の形にすれば計算できる! 3 整数に このペンキ1dLでは、何m²ぬれますか。 どんな式になりますか。 昨日の問題と同じで、1dLを求めている。 式は、 4 9 4 9 ÷ 2 3 2 3 です。 分数×分数の計算は、分子と分母をそれぞれかけて求めることができたので、同じように考えてみよう。 4÷2 9÷3 4 ÷ 2 9 ÷ 3 = 2 3 2 3 分数÷分数も同じように、分子同士と分母同士をそれぞれをわれば、できるね。 この方法は、いつ無料でダウンロード・プリントアウトできる小学生用・算数の単位換算表 です。 小学校で習う、時間、長さ、かさ、重さ、面積、体積の単位の一覧、早見表を作ってみました。 関連ページ ⇒小学6年生 いろいろな単位・単位の計算 問題プリント




小5 算数 小5 30 2 分数と小数 整数の関係 Youtube



4年算数 分数 1 わかる教え方のポンイト
分数 ・単位量に満たない端数部分の大 きさを分数を用いて表すこと ・1/10の位の用語 小数と整数のしくみ ・小数の表現を広げて表すこと (小数第二位,小数第三位,1/100 の位,1/1000の位) ・小数の位取りの原理 小数のかけ算とわり算 ・小数×整数の計算分数の足し算(分母9まで) 分数の足し算(分母2桁1) 分数の足し算(分母2桁2) 分数の引き算 約分しない分数の引き算;小数のしくみ ・小数の意味の拡張 ・小数の加減計算とその筆 算 分数 ・単位量に満たない端数部 分の大きさを分数を用 いて表すこと ・「真分数」「仮分数」「帯 分数」の意味 ・大きさの等しい分数 ・帯分数を含む同分母分数 の加減計算 分数分数



小学算数 構造的板書 の工夫とコツ 分数のたし算 ひき算 みんなの教育技術




帯分数の足し算 分母が同じ 繰り上がりあり 計算ドリル 問題集 数学fun
2.分数のかき方の指導 (1)分数のしくみ 1を2等分した1つ分を1 ,1を3等 分した2つ分を2 というように表した ものを分数という。 (2)分数の読み方 「(分母)分の(分子)」と分母を先に 読み,続いて分子を 読む。例えば,右の 分数は「五分の四」 と読む。・分数の意味と表し方 等を等分する活動を行い、等しく分ける表し方についての 動 1 ・かさも分数で表せること 興味・関心を高める。 ~ ・「 」 」分数「分母「分子」 1mにたりない端数部分の長さをmを使って表すことを操 算数的活4年算数 分数(1)わかる教え方 これまでに習ってきた分数を忘れている時には、前の学年のおさらいをするとわかりやすくなります 「3年の分数のおさらい」 「2年の分数のおさらい」 ①1より大きい分数の表し方 ②仮分数と帯分数の意味と表し方 ③




こどもプリント 小学3年生の分数計算問題 引き算 無料プリント 小学3年生 小学 分数




小学3年生 算数 無料問題集 分母が同じ分数の足し算 おかわりドリル
・分数を用いると、整 数で表せない等分し てできる部分の大き さや端数部分の大き さを表せるよさに気 づき、生活や学習に 用いようとしてい る。 ・分数は都合に応じて 単位量をn等分した 1こ分を単位として いることをとらえ、 分数の表し方や分数 分数とは何かを「式」で理解する 1つのもの を、 に等しく分けた(÷ )、〇個分(×〇)ですから、これを式に表してみると、 〇 〇 となります。 1つのものの"1"を、上の図では1つの円で考えましたが、 でも でもリボンでもなんでもよいのです。 ですが、 大きさの違うもの同士の"1"は、一緒に考えてはいけません。 下の図では、オレンジの四角と緑の丸は分数, 数 もとになる分数をたしあわせてみよう 1.「分母を変える」ボタンで1を何等分かします 2.「もとにする分数」ボタンをおすともとにする分数があらわれます 3.「たす」ボタンをおしてもとにする分数をたしあわせていきます



3年算数プリント 分数3



分数 小6 分数 分数 算数の教え方教えますmother S Math Happy Study Support
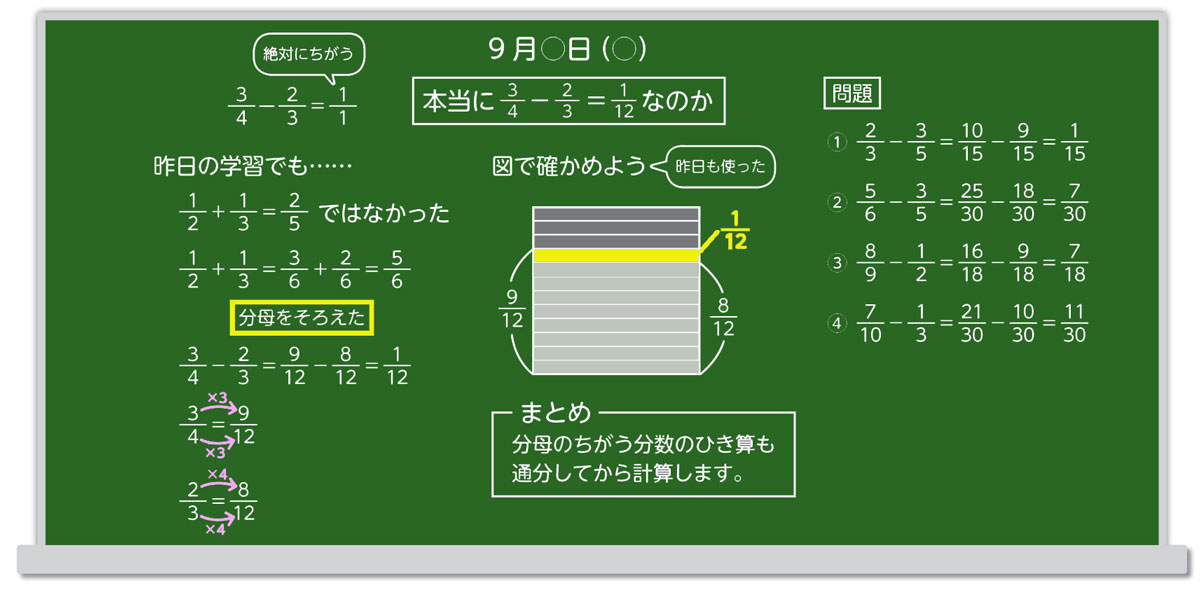
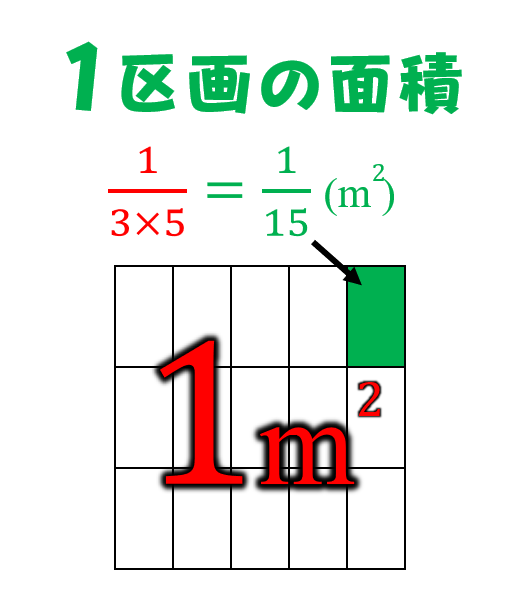
分数+分数の計算のしかたを考えよう。 見通し 小数の05+03のときは、01を基にして考えたので、今回も基にする数を決めて、その数のいくつ分と考えればよいと思います。 図や数直線に表して考えればよいと思います。 第 6 回のテーマは「 分数の概念と計算方法 」です。 割り算 , 割合 , 比の「 変形 」である「 分数 」についての話です。 今までの「 割り算 , 割合 , 比 」の知識 は、この「 分数 」を理解することで 全てが繋がり、完成します 。 分数は小数とも密接な関わりがあります。(1) 分数 1m のテープを同じ長さに3つに分けて,リボンをつくります。 同じ大きさに3つに分けることを,3等分すると いいます。 1mを3等分した1つ分の長さを,1mの三分の一といいます。
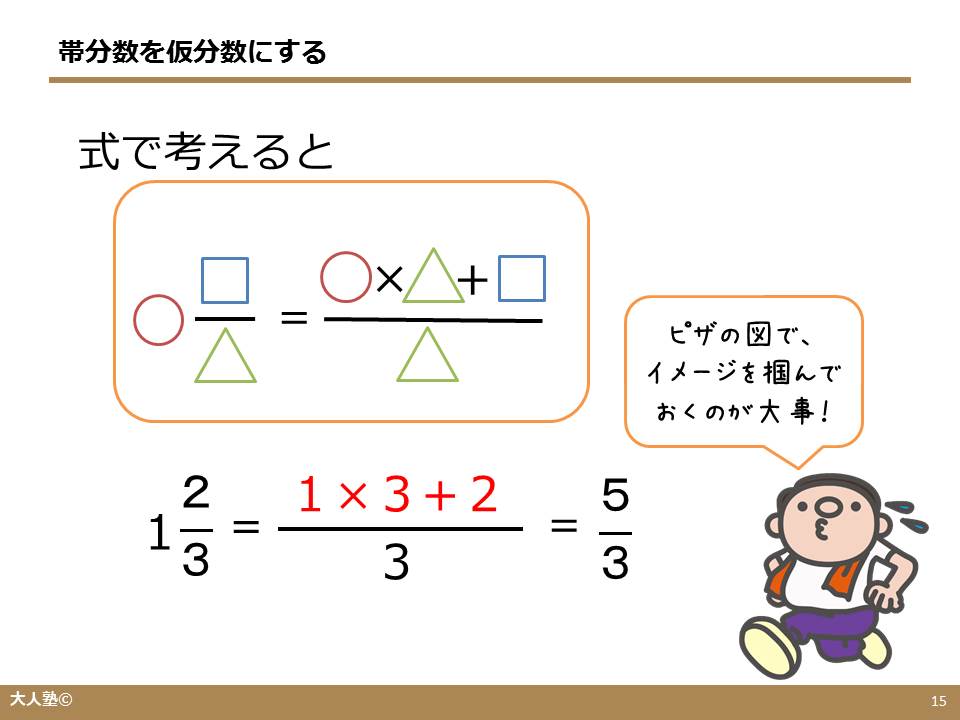



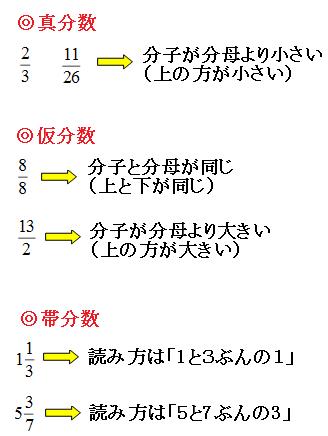
真分数 仮分数 帯分数とは 大人の学び直し算数 計算のやり方解説 無料




6年算数分数 分数 わかる教え方
(6)分数の意味や表し方について理解できるようにする。 ア 等分してできる部分の大きさや端数部分の大きさを表すのに分数を用いること。また、分 数の表し方についてしること。 イ 分数は、単位分数のいくつ分かで表せることを知ること。6年算数 分数×分数 子どもの学習支援 by いっちに算数 スマホ版 フリー素材提供 分数×分数の計算の考え方をわかりやすくするために、このサイトでは、下のような算数アニメを用いています。 ※アニメの説明は記事中にありますので、ここでは参考にご覧下さい。管理人 9月 16, 18 / 10月 22, 18 『分数×分数』の掛け算は分母同士・分子同士かけて答えを求めます。 大人にしてみれば当たり前の計算ですが、なぜこのように計算するのかを子どもに的確に説明するのはとても困難です。 計算方法だけ教えてあげるというのも手ですが、分数の掛け算は今後算数・数学を学ぶ上で欠かせないツールになるので、ぜひとも根本的に



1




部分分数分解のやり方と公式 5パターンの問題から分かる変形のコツ アタリマエ
分数 の加減計算 について ,第6学年第 3単元 で異分母分数 の加減計算 について ,それぞれ 学習 してきている 。本単元 では ,分数 のしくみなどの 理解 の上に,分数 に整数 をかける 乗




分数 小数の変換方法 小学生に教えるための分かりやすい解説 数学fun
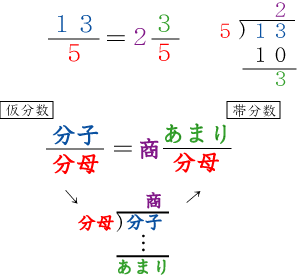



仮分数 帯分数 4年生 算数の広場



6年算数分数 分数 逆数 割合 教え方




動画で学習 1 分数 算数



2
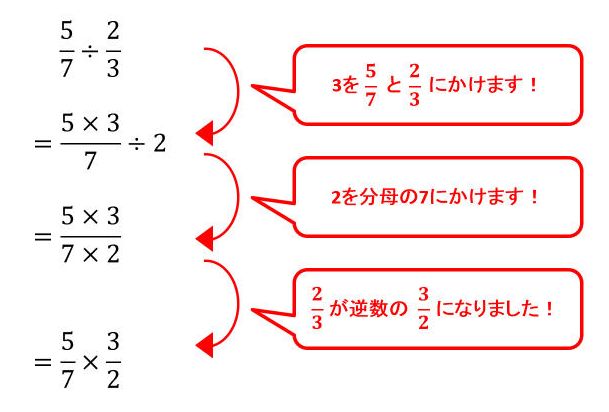



分数のわり算の仕組みを理解しよう 逆数をかけるのはどうして の謎に挑む 中学受験ナビ
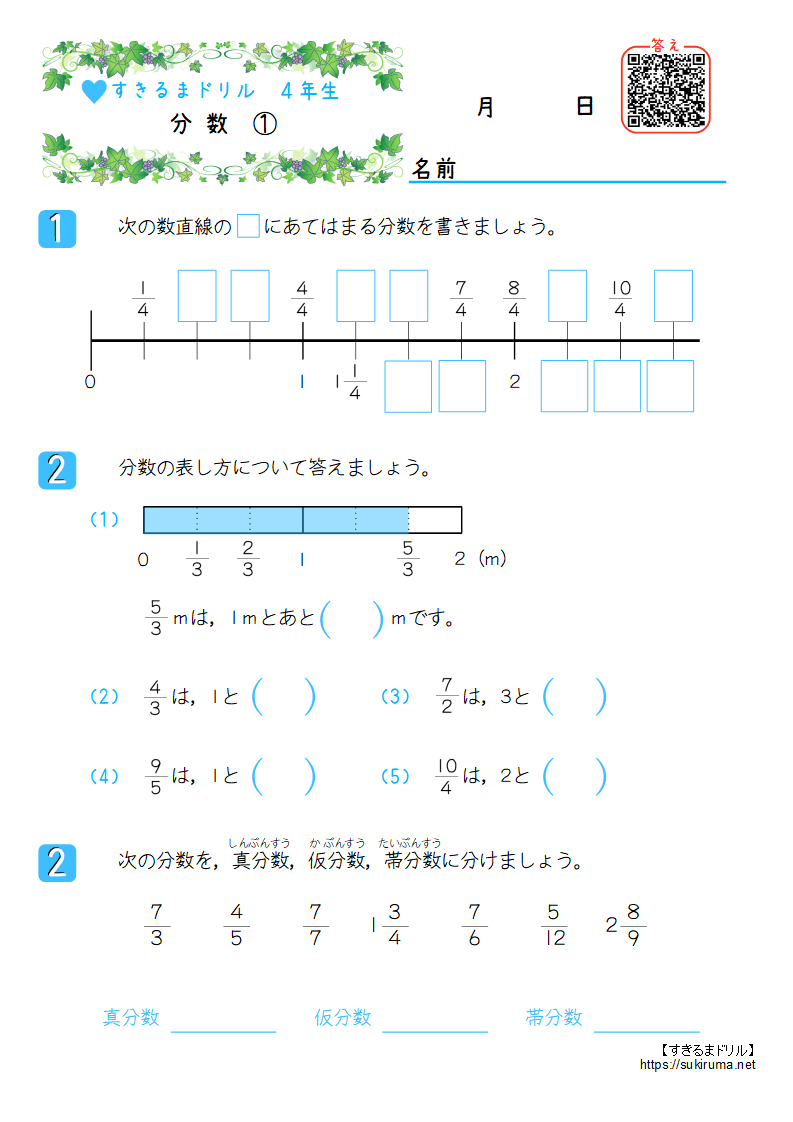



すきるまドリル 小学4年生 算数 分数 無料学習プリント すきるまドリル 無料学習プリント
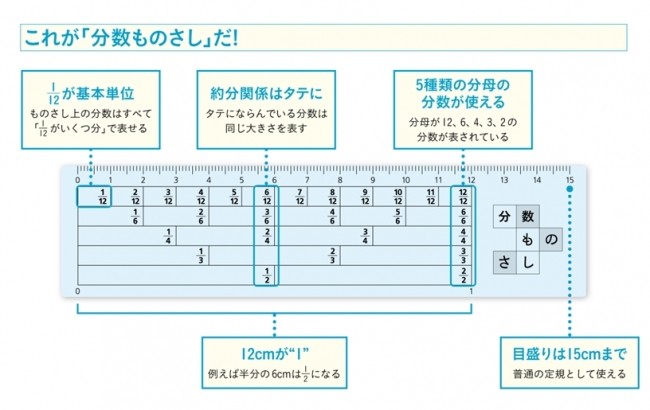



教育者も注目する発明 各メディアでも話題騒然 小学5年生 当時 山本賢一朗君考案 分数を直感的に習得できる魔法の教材 分数 ものさし 待望の新発売 株式会社プレジデント社のプレスリリース




ページタイトル




分数の掛け算の上手な教え方 なぜ分母同士 分子同士をかけるのか 数学fun



2




算数 分数の仕組み 小学生 算数のノート Clear
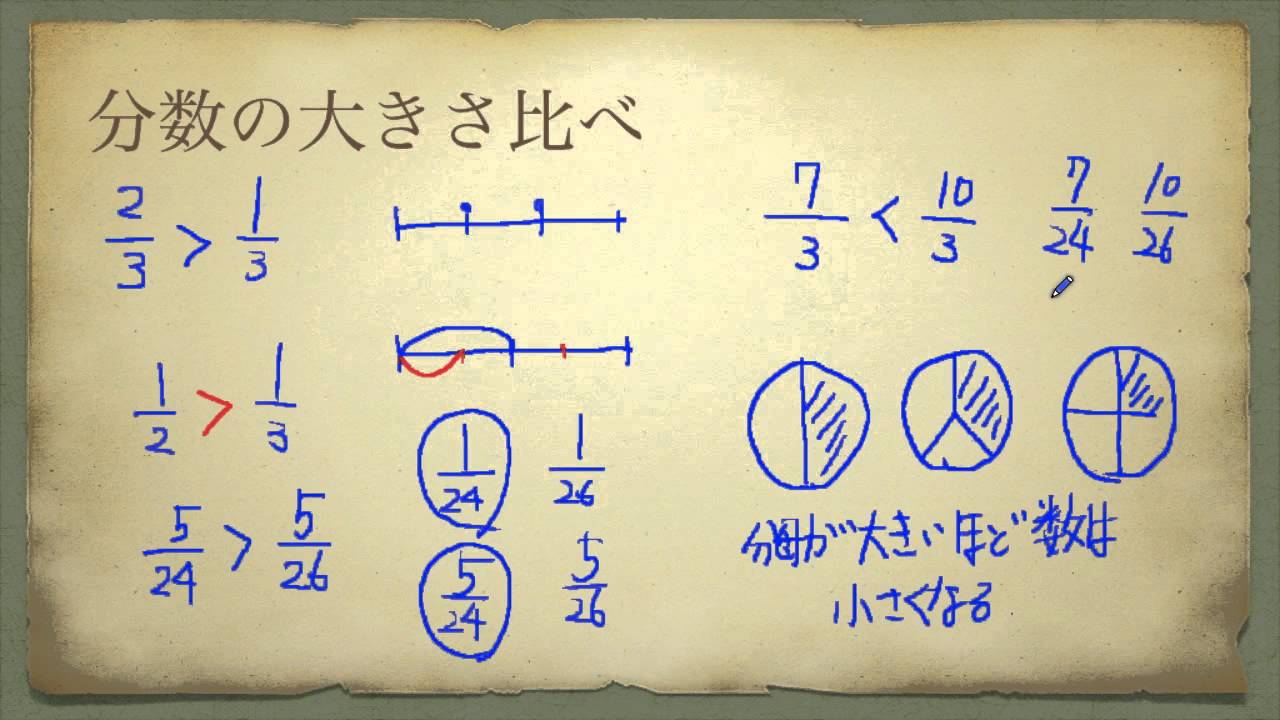



小学校4年 算数 分数の大きさ比べ Youtube



記事 詳細情報 21年 2月 19日 金曜日 4年ニュース 4年 分数のしくみを調べよう 算数の学習で ジャンケンをし 勝ったらピザが手に入れられるゲームを行いました 最後に手元に残ったピザの枚数を分数で表します 真分数 仮分数 帯分数など



6年算数分数 分数 わかる教え方




算数も怪しい人が知りたかった分数計算の真髄 子育て 東洋経済オンライン 社会をよくする経済ニュース



1



4年算数 分数 1 わかる教え方のポンイト




分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利
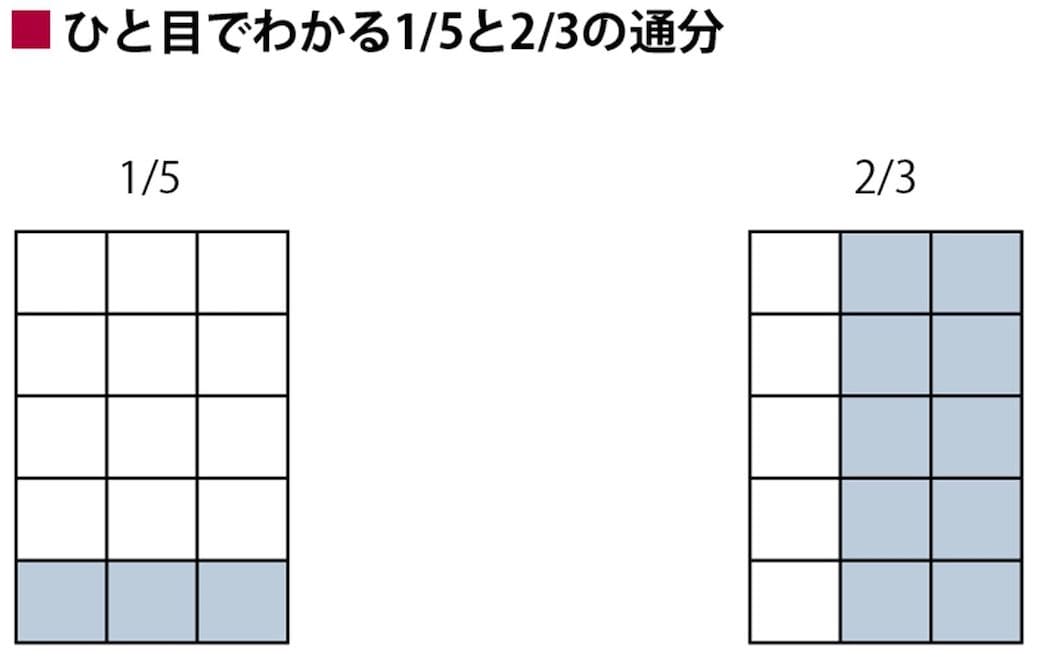



算数も怪しい人が知りたかった分数計算の真髄 子育て 東洋経済オンライン 社会をよくする経済ニュース



小学3年生で習う分数は 分数の意味 数直線など そうちゃ式 分かりやすい図解算数 別館




1 Descubre Como Resolverlo En Qanda



記事 詳細情報 17年 12月 15日 金曜日 3年生 算数の授業 3年生は算数の時間に分数を学習しています この日はまとめのテストを行いました 確実に理解できるように指導 支援していきます 14時57分




小学3年生 算数 無料問題集 分母が同じ分数の足し算 おかわりドリル




帯分数の計算方法と仮分数への書き直し方




小3算数 p 39 分数 分数のしくみと数直線 Youtube
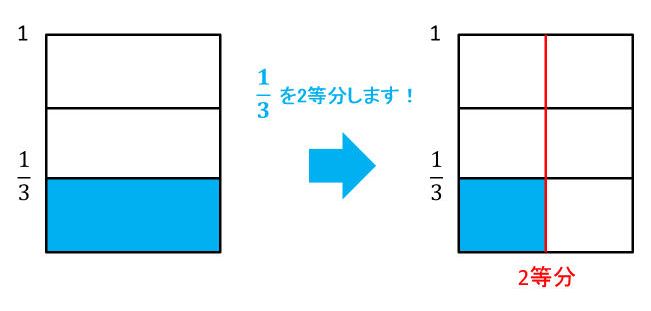



分数のわり算の仕組みを理解しよう 逆数をかけるのはどうして の謎に挑む 中学受験ナビ




4年生算数ドリル 分数
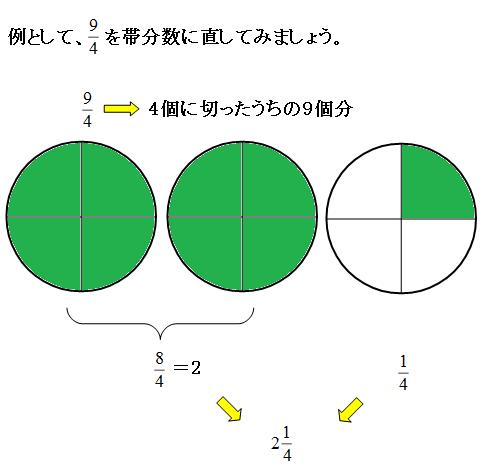



分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利




分数がわかる できる 教えられる 漫画 無料試し読みなら 電子書籍ストア ブックライブ




小学3年生 文章問題 分数の計算 練習プリント テスト ちびむすドリル 小学生




ドイツ語 英語de 数 大特集 数字 算数 分数 少数 図形 どう言う 完全版 ドイツgogaku
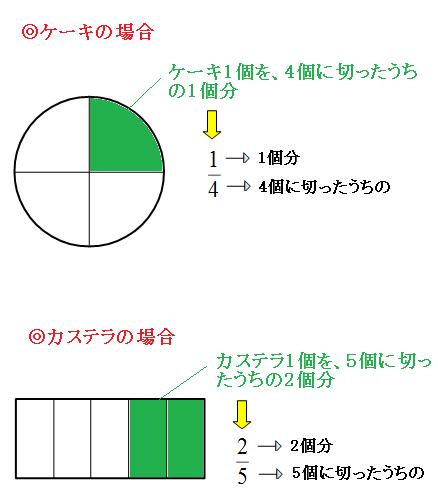



分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利




分数の掛け算の上手な教え方 なぜ分母同士 分子同士をかけるのか 数学fun
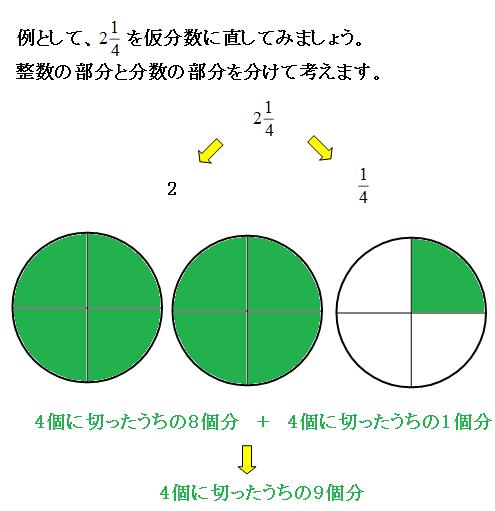



分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利




分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利




何で分数の割り算は逆数をかけるの 理由を説明できますか
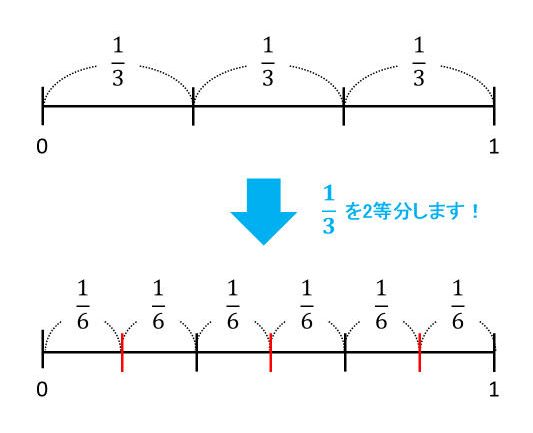



分数のわり算の仕組みを理解しよう 逆数をかけるのはどうして の謎に挑む 中学受験ナビ
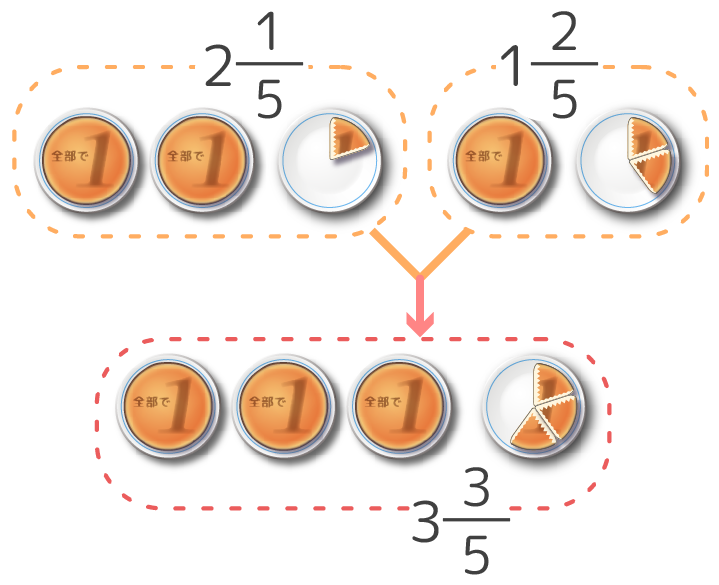



小学4年生 帯分数の足し算引き算 分数のくり上がり くり下がりも そうちゃ式 分かりやすい図解算数 別館




分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ
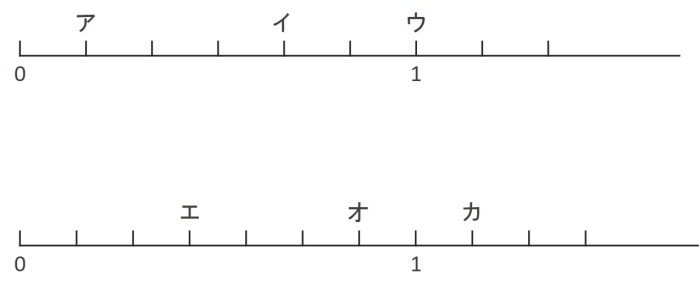



動画で学習 2 分数のしくみ 算数
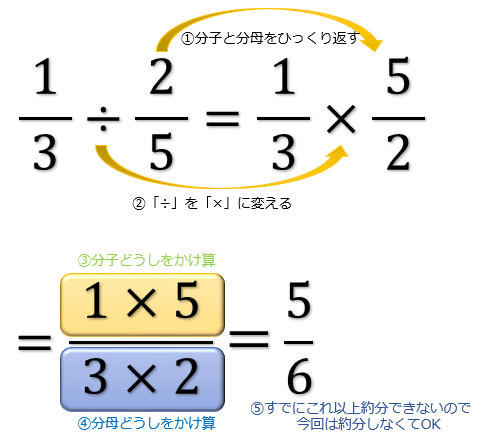



分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ




小4算数 分数 仮分数と帯分数のかきかえ 勉強 Youtube スタディチューブ



算数4年から6年




分数の名前を覚えて分数攻略 ふるやまんのマスラボ奮闘記
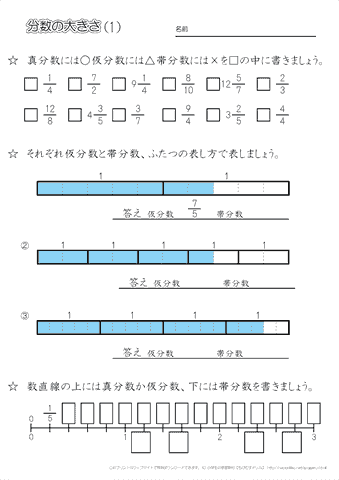



小学生の算数 分数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 小学生



分数の掛け算の上手な教え方 なぜ分母同士 分子同士をかけるのか 数学fun



小6算数 分数のわり算 指導アイデア みんなの教育技術



真分数 仮分数 帯分数とは 大人の学び直し算数 計算のやり方解説 無料




6年算数 分数 分数 アニメでわかりやすく 学習支援サイト いっちに算数 のブログ




4年生算数ドリル 分数




小学5年生の算数 分数の約分 通分 練習問題プリント ちびむすドリル 小学生




算数 分数の仕組み 小学生 算数のノート Clear



小3 算数 小3 51 分けた大きさの表し方 分数 Youtube



Qb説明 算数 3年 分数 On The App Store




夢中で算数 をつくる教材アイディア集 横山験也 本 通販 Amazon




帯分数の計算方法と仮分数への書き直し方
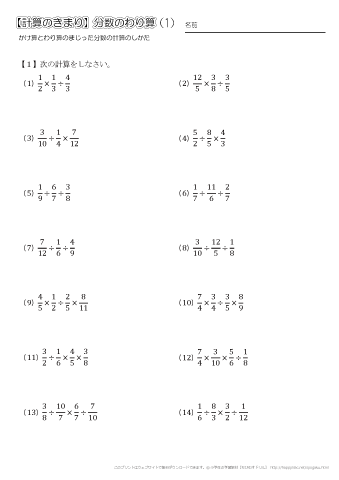



小学生の算数 分数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 小学生
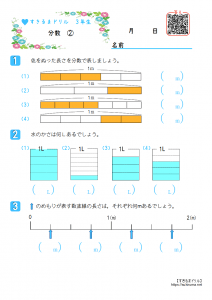



すきるまドリル 小学3年生算数 分数 無料学習プリント すきるまドリル 無料学習プリント



Www Education Fukaya Saitama Jp Action Common Download Main Upload Id




分数の割り算はなぜひっくり返してかけるのか その理由を解説 空間情報クラブ 株式会社インフォマティクス




分数のかけ算わり算 まとめ 小学生 算数のノート Clear
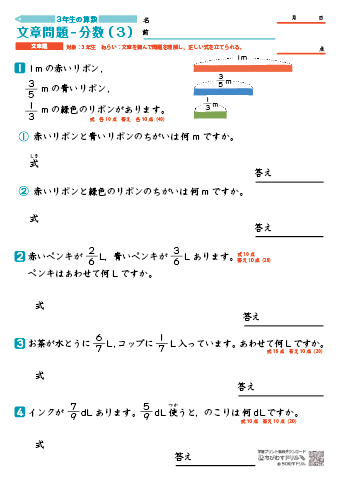



小学3年生 文章問題 分数の計算 練習プリント テスト ちびむすドリル 小学生
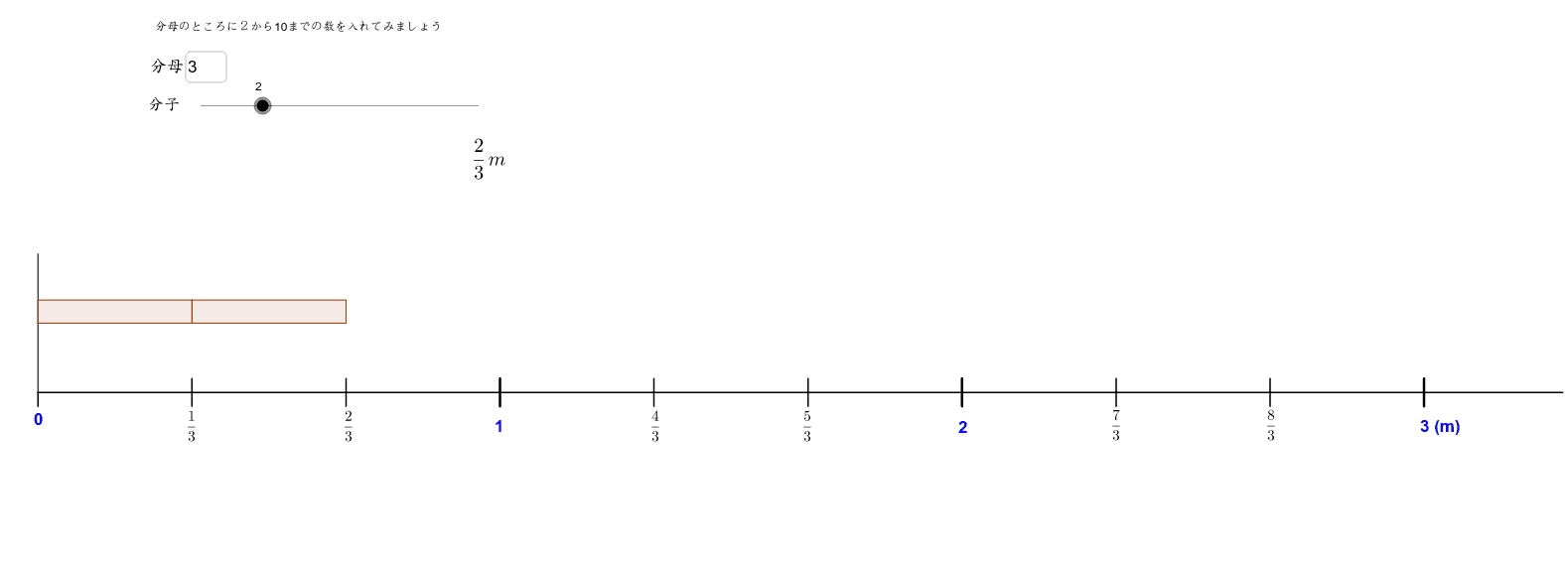



分数のしくみ 仮分数 帯分数編 Geogebra




分数の割り算の仕組みを絵で表現するには 映画おもひでぽろぽろで 数学 教えて Goo
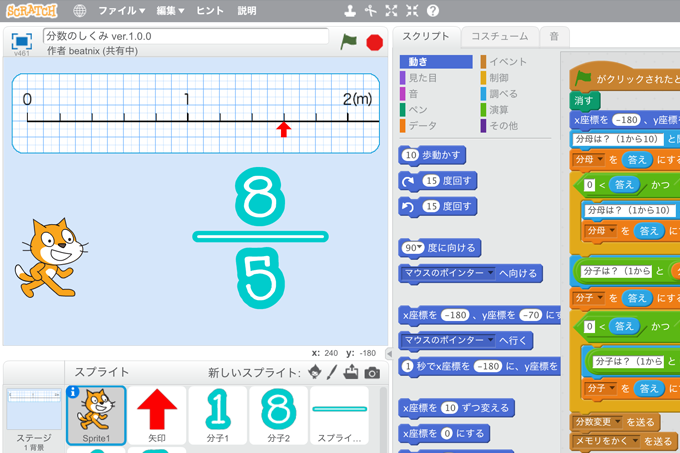



既存の教科でプログラミング授業 小学3年生 算数 分数のしくみ コドモとアプリ




Amazon Co Jp 3分の2を4分の1で割るって どういうこと なるほど 君にもきっとわかる 分数の割り算の仕組みを 独自の切り口で解説した本 Ebook 田中 智之 本




分数のわり算の仕組みを理解しよう 逆数をかけるのはどうして の謎に挑む 中学受験ナビ




帯分数 仮分数の変換の練習問題 計算ドリル 問題集 数学fun




小学校3年生動画 分数のしくみを知ろう ふるやまんのマスラボ奮闘記
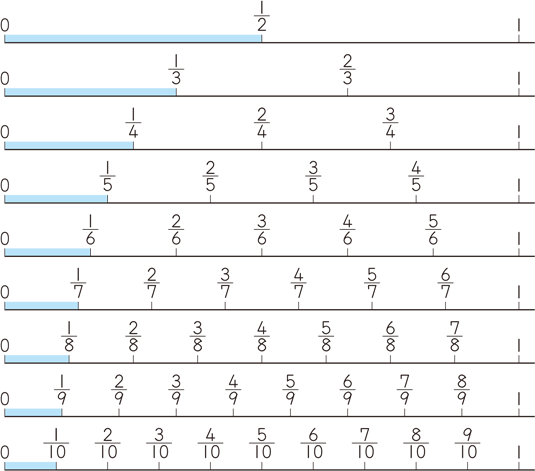



単位分数と分数の性質 算数用語集




算数 分数と小数と整数 小学生 算数のノート Clear



1




帯分数 仮分数の変換方法 小学生に教えるための分かりやすい解説 数学fun




小学生の算数 分数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 小学生




6年算数分数 分数 わかる教え方



1



6年算数分数 分数 わかる教え方




分数 分数の表し方からかけ算わり算まで くもん出版




分数の概念と計算方法
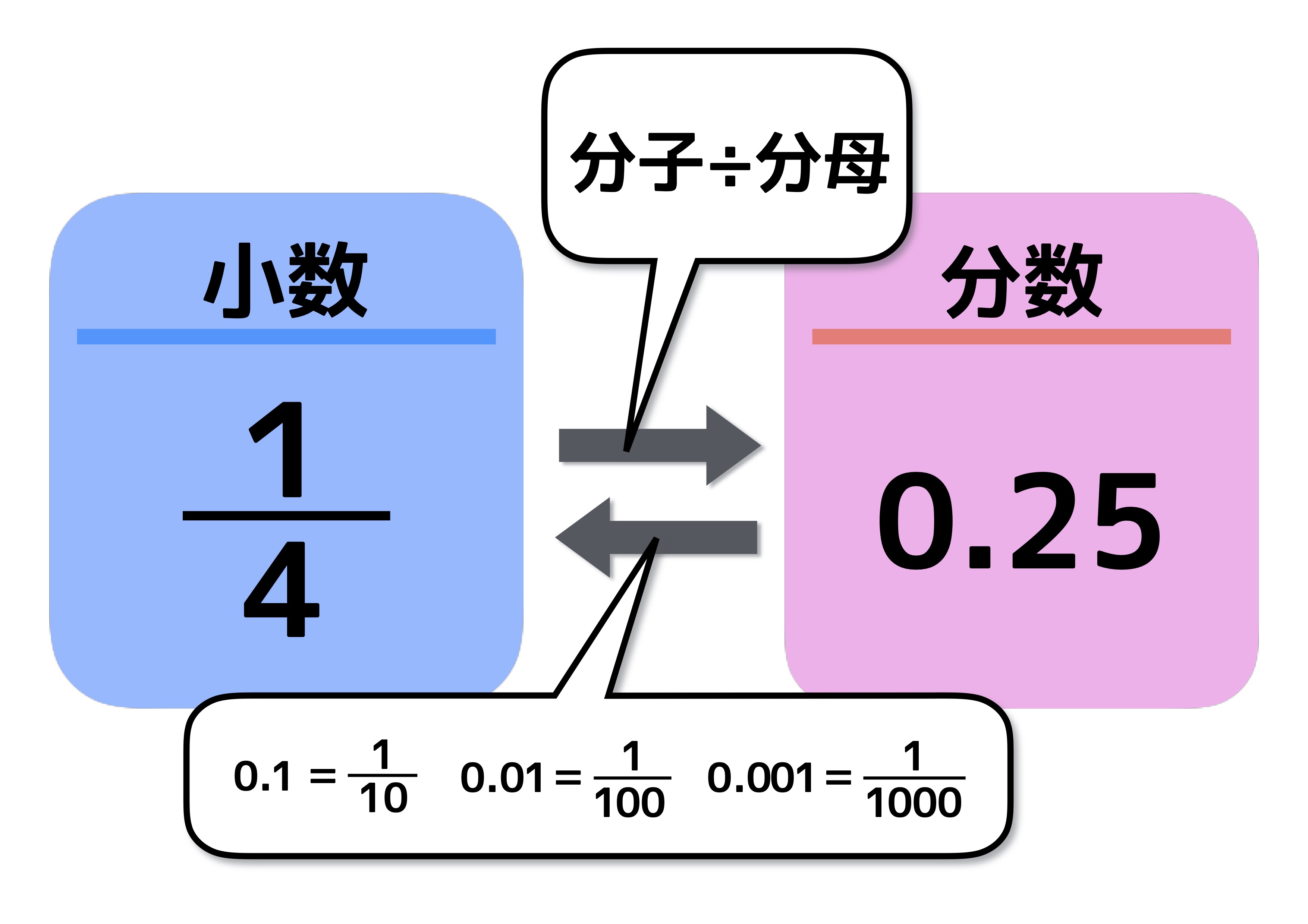



分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ




親子ではじめる算数つまずき練習帳 読むだけで小数 分数 かさ 割合 百分率のしくみがたちまちわかる お母さん もっとおしえて シリーズ Shoi Ko Yoshimoto Amazon Com Books
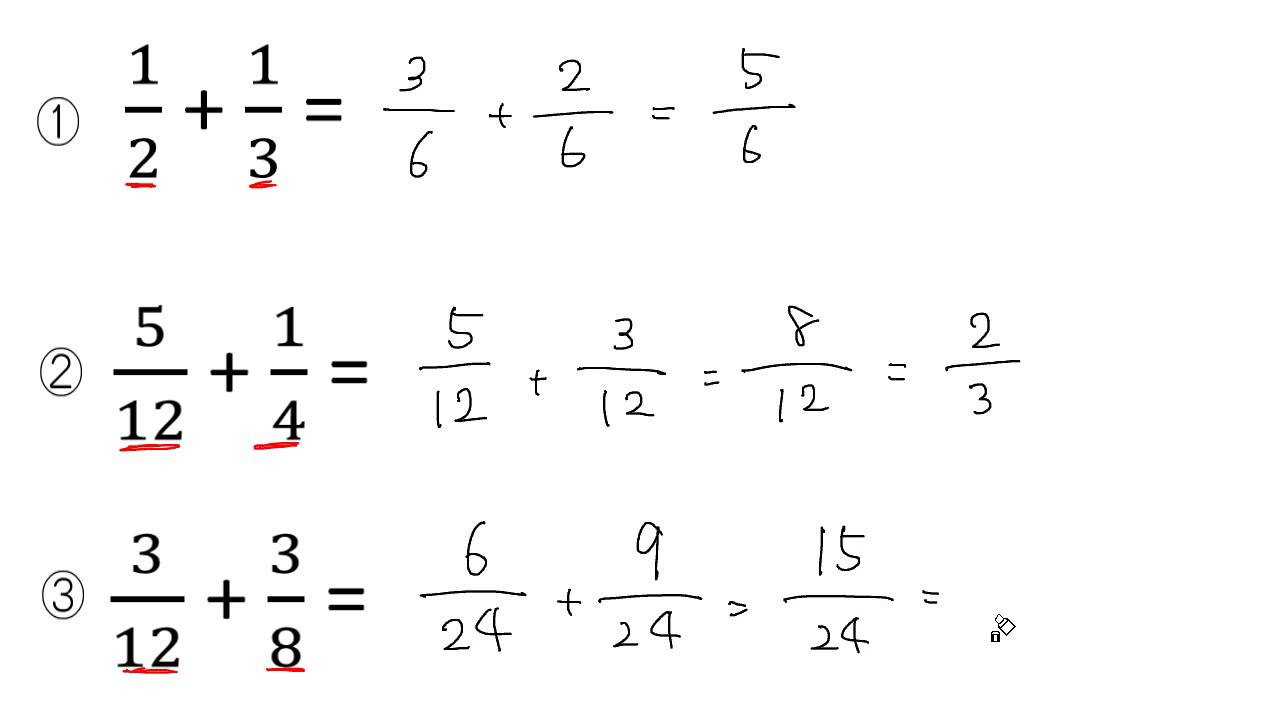



分数の足し算 引き算 通分あり Youtube




教育者も注目する発明 各メディアでも話題騒然 小学5年生 当時 山本賢一朗君考案 分数を直感的に習得できる魔法の教材 分数 ものさし 待望の新発売 株式会社プレジデント社のプレスリリース
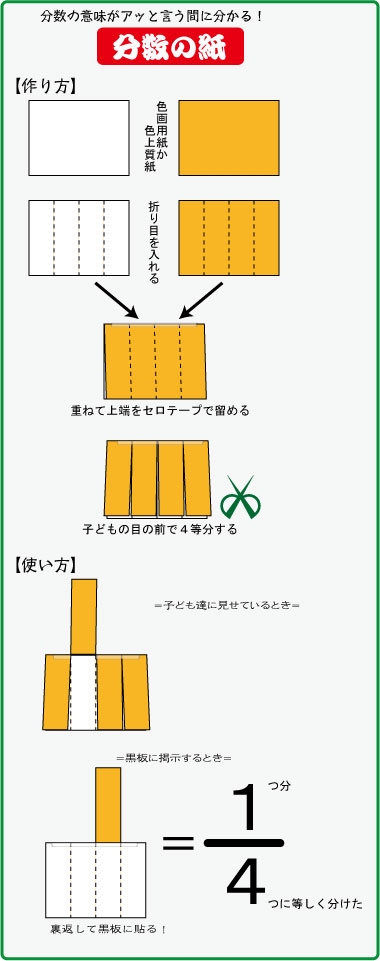



分数の意味が一目で分かる 分数の紙 嗚呼 懐かしい さくら社



Http Www City Hachioji Tokyo Jp Kurashi Kyoiku 003 004 001 P D Fil 28q A 4 Pdf




動画で学習 2 分数のしくみ 算数




算数のほんねシリーズの販売 教材出版 学林舎




6年算数分数 分数 わかる教え方




既存の教科でプログラミング授業 小学3年生 算数 分数のしくみ コドモとアプリ


